Глава 8.1. Подготовка за практически изпит – част I
В настоящата глава ще разгледаме няколко задачи с ниво на трудност, каквото може да очаквате от задачите на практическия изпит по “Основи на програмирането”. Ще преговорим и упражним всички знания, които сте придобили от настоящата книга и през курса "Programing Basics".
Видео
Практически изпит по “Основи на програмирането”
Курсът "Programing Basics" приключва с практически изпит. Включени са 6 задачи, като ще имате 4 часа, за да ги решите. Всяка от задачите на изпита ще засяга една от изучаваните теми по време на курса. Темите на задачите са както следва:
- Задача с прости сметки (без проверки)
- Задача с единична проверка
- Задача с по-сложни проверки
- Задача с единичен цикъл
- Задача с вложени цикли (чертане на фигурка на конзолата)
- Задача с вложени цикли и по-сложна логика
Система за онлайн оценяване (Judge)
Всички изпити и домашни се тестват автоматизирано през онлайн Judge система: https://judge.softuni.org. За всяка от задачите има открити (нулеви) тестове, които ще ви помогнат да разберете какво се очаква от задачата и да поправите грешките си, както и състезателни тестове, които са скрити и проверяват дали задачата ви работи правилно. В Judge системата се влиза с вашия softuni.bg акаунт.
Как работи тестването в Judge системата? Качвате сорс кода и от менюто под него избирате да се изпълни с JavaScript. Програмата бива тествана с поредица от тестове, като за всеки успешен тест получавате точки.
Задачи с прости пресмятания
Първата задача на практическия изпит по “Основи на програмирането” обхваща прости пресмятания без проверки и цикли. Ето няколко примера:
Задача: лице на триъгълник в равнината
| Триъгълник в равнината е зададен чрез координатите на трите си върха. Първо е зададен върхът (x1, y1). След това са зададени останалите два върха: (x2, y2) и (x3, y3), които лежат на обща хоризонтална права (т.е. имат еднакви Y координати). Напишете програма, която пресмята лицето на триъгълника по координатите на трите му върха. |
|
Входни данни
Като параметри на функцията подаваме 6 цели числа: x1, y1, x2, y2, x3, y3.
- Всички числа са в диапазона [-1000 … 1000].
- Гарантирано е, че y2 = y3.
Изходни данни
Да се отпечата на конзолата лицето на триъгълника.
Примерен вход и изход
| Вход | Изход | Чертеж | Обяснения |
|---|---|---|---|
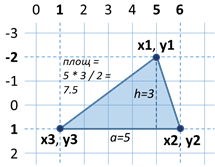
| 5 -2 6 1 1 1 |
7.5 |  |
Страната на триъгълника а = 6 - 1 = 5 Височината на триъгълника h = 1 - (-2) = 3 Лицето на триъгълника S = a * h / 2 = 5 * 3 / 2 = 7.5 |
| Вход | Изход | Чертеж | Обяснения |
|---|---|---|---|
| 4 1 -1 -3 3 -3 |
8 | 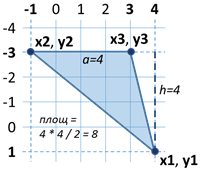 |
Страната на триъгълника а = 3 - (-1) = 4 Височината на триъгълника h = 1 - (-3) = 4 Лицето на триъгълника S = a * h / 2 = 4 * 4 / 2 = 8 |
Насоки и подсказки
Изключително важно при подобен тип задачи, при които се подават някакви координати, е да обърнем внимание на реда, в който се подават, както и правилно да осмислим кои от координатите ще използваме и по какъв начин. В случая, на входа се подават x1, y1, x2, y2, x3, y3 в този си ред. Ако не спазваме тази последователност, решението става грешно. Първо пишем кода, който чете подадените данни:
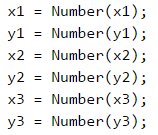
Трябва да пресметнем страната и височината на триъгълника. От примерите, както и от условието y2 = y3 забелязваме, че едната страна винаги е успоредна на хоризонталната ос. Това означава, че нейната дължина е равна на дължината на отсечката между нейните координати x2 и x3, която е равна на разликата между по-голямата и по-малката координата. Аналогично можем да изчислим и височината. Тя винаги ще е равна на разликата между y1 и y2(или y3, тъй като са равни). Тъй като не знаем дали винаги x2 ще е по-голям от x3, или y1 ще е под или над страната на триъгълника, ще използваме абсолютните стойности на разликата, за да получаваме винаги положителни числа, понеже една отсечка не може да има отрицателна дължина.

По познатата ни от училище формула за намиране на лице на триъгълник ще пресметнем лицето.
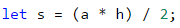
Единственото, което остава, е да отпечатаме лицето на конзолата.
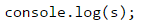
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#0.
Задача: пренасяне на тухли
Строителни работници трябва да пренесат общо x тухли. Работниците са w на брой и работят едновременно. Те превозват тухлите в колички, всяка с вместимост m тухли. Напишете програма, която прочита целите числа x, w и m и пресмята колко най-малко курса трябва да направят работниците, за да превозят тухлите.
Входни данни
Като параметри на функцията подаваме 3 цели числа:
- Броят тухли x
- Броят работници w
- Вместимостта на количката m
Всички входни числа са цели и в диапазона [1 … 1000].
Изходни данни
Да се отпечата на конзолата минималният брой курсове, необходими за превозване на тухлите.
Примерен вход и изход
| Вход | Изход | Обяснения |
|---|---|---|
| 120 2 30 |
2 | Имаме 2 работника, всеки вози по 30 тухли на курс. Общо работниците возят по 60 тухли на курс. За да превозят 120 тухли, са необходими точно 2 курса. |
| Вход | Изход | Обяснения |
|---|---|---|
| 355 3 10 |
12 | Имаме 3 работника, всеки вози по 10 тухли на курс. Общо работниците возят по 30 тухли на курс. За да превозят 355 тухли, са необходими точно 12 курса: 11 пълни курса превозват 330 тухли и последният 12-ти курс пренася последните 25 тухли. |
| Вход | Изход | Обяснения |
|---|---|---|
| 5 12 30 |
1 | Имаме 5 работника, всеки вози по 30 тухли на курс. Общо работниците возят по 150 тухли на курс. За да превозят 5 тухли, е достатъчен само 1 курс (макар и непълен, само с 5 тухли). |
Насоки и подсказки
Входът е стандартен, като единствено трябва да внимаваме за последователността, в която прочитаме данните.
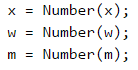
Пресмятаме колко тухли носят работниците на един курс.
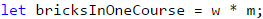
Като разделим общия брой на тухлите, пренесени за 1 курс, ще получим броя курсове, необходими за пренасянето им. Ще използваме методаMath.ceil(…), за да закръглим получения резултат винаги нагоре. Когато тухлите могат да се пренесат с точен брой курсове, делението ще връща точно число и няма да има нищо за закръгляне. Съответно, когато не е така, резултатът от делението ще е броя на точните курсове, но с десетична част. Десетичната част ще се закръгли нагоре и така ще се получи нужният 1 курс за оставащите тухли.
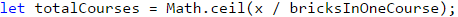
Накрая принтираме резултата на конзолата.
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#1.
Задачи с единична проверка
Втората задача на практическия изпит по “Основи на програмирането” обхваща условна конструкция и прости премятания. Ето няколко примера:
Задача: точка върху отсечка
Върху хоризонтална права е разположена хоризонтална отсечка, зададена с x координатите на двата си края: first и second. Точка е разположена върху същата хоризонтална права и е зададена с x координатата си. Напишете програма, която проверява дали точката е вътре или вън от отсечката и изчислява разстоянието до по-близкия край на отсечката.
Входни данни
Като параметри на функцията подаваме 3 цели числа:
- Числото first – единия край на отсечката.
- Числото second – другия край на отсечката.
- Числото point – местоположението на точката.
Всички входни числа са цели и в диапазона [-1000 … 1000].
Изходни данни
Резултатът да се отпечата на конзолата:
- На първия ред да се отпечата "in" или "out" – дали точката е върху отсечката или извън нея.
- На втория ред да се отпечата разстоянието от точката до най-близкия край на отсечката.
Примерен вход и изход
| Вход | Изход | Визуализация |
|---|---|---|
| 10 5 7 |
in 2 |
 |
| Вход | Изход | Визуализация |
|---|---|---|
| 8 10 5 |
out 3 |
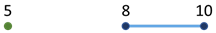 |
| Вход | Изход | Визуализация |
|---|---|---|
| 1 -2 3 |
out 2 |
 |
Насоки и подсказки
Четем входа от конзолата.
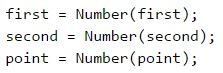
Тъй като не знаем коя точка е от ляво и коя е от дясно, ще си направим две променливи, които да ни отбелязват това. Тъй като лявата точка е винаги тази с по-малката х координата, ще ползваме Math.min(…), за да я намерим. Съответно, дясната е винаги тази с по-голяма х координата и ползваме Math.max(…). Ще намерим и разстоянието от точката x до двете точки. Понеже не знаем положението им една спрямо друга, ще използваме Math.abs(…), за да получим положителен резултат.
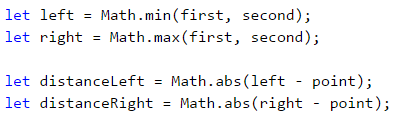
По-малкото от двете разстояния ще намерим ползвайки Math.min(…).
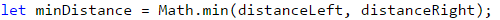
Остава да намерим дали точката е на линията или извън нея. Точката ще се намира на линията винаги, когато тя съвпада с някоя от другите две точки или х координатата ѝ се намира между тях. В противен случай, точката се намира извън линията. След проверката изкарваме едното от двете съобщения, спрямо това коя проверка е удовлетворена.

Накрая принтираме разстоянието, намерено преди това.
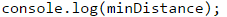
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#2.
Задача: точка във фигура
Да се напише програма, която проверява дали дадена точка (с координати x и y) е вътре или извън следната фигура:
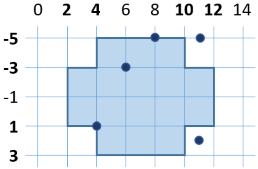
Входни данни
Като параметри на функцията подаваме две цели числа: x и y.
Всички входни числа са цели и в диапазона [-1000 … 1000].
Изходни данни
Да се отпечата на конзолата "in" или "out" – дали точката е вътре или извън фигурата (на контура е вътре).
Примерен вход и изход
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 8 -5 |
in | 6 -3 |
in |
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 11 -5 |
out | 11 2 |
out |
Насоки и подсказки
За да разберем дали точката е във фигурата, ще разделим фигурата на 2 четириъгълника:
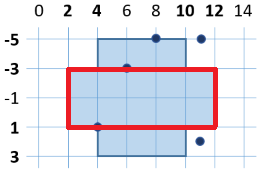
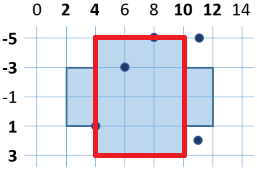
Достатъчно условие е точката да се намира в един от тях, за да се намира във фигурата.
Четем от конзолата входните данни:
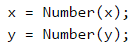
Ще създадем две променливи, които ще отбелязват дали точката се намира в някой от правоъгълниците.
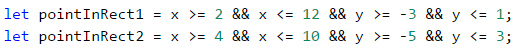
При отпечатването на съобщението ще проверим дали някоя от променливите е приела стойност true. Достатъчно е само една от тях да е true, за да се намира точката във фигурата.

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#3.
Задачи с по-сложни проверки
Третата задача на практическия изпит по “Основи на програмирането” включва няколко вложени проверки съчетани с прости пресмятания. Ето няколко примера:
Задача: дата след 5 дни
Дадени са две числа d (ден) и m (месец), които формират дата. Да се напише програма, която отпечатва датата, която ще бъде след 5 дни. Например 5 дни след 28.03 е датата 2.04. Приемаме, че месеците: април, юни, септември и ноември имат по 30 дни, февруари има 28 дни, а останалите имат по 31 дни. Месеците да се отпечатат с водеща нула, когато са едноцифрени (например 01, 08).
Входни данни
Като параметри на функцията подаваме две цели числа:
- Цяло число d в интервала [1 … 31] – ден. Номерът на деня не надвишава броя дни в съответния месец (напр. 28 за февруари).
- Цяло число m в интервала [1 … 12] – месец. Месец 1 е януари, месец 2 е февруари, …, месец 12 е декември. Месецът може да съдържа водеща нула (напр. април може да бъде изписан като 4 или 04).
Изходни данни
Отпечатайте на конзолата един единствен ред, съдържащ дата след 5 дни във формат ден.месец. Месецът трябва да бъде двуцифрено число с водеща нула, ако е необходимо. Денят трябва да е без водеща нула.
Примерен вход и изход
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 28 03 |
2.04 | 27 12 |
1.01 |
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 25 1 |
30.01 | 26 02 |
3.03 |
Насоки и подсказки
Приемаме си входа от конзолата.
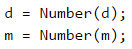
За да си направим по-лесно проверките, ще си създадем една променлива, която ще съдържа броя дни, които има в месеца, който сме задали.
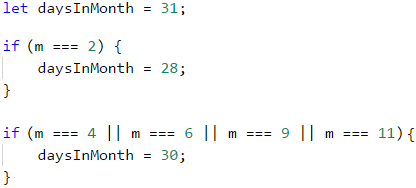
Увеличаваме деня с 5.
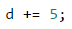
Проверяваме дали денят не е станал по-голям от броя дни, които има в съответния месец. Ако това е така, трябва да извадим дните от месеца от получения ден, за да получим нашият ден на кой ден от следващия месец съответства.
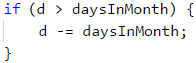
След като сме минали в следващия месец, това трябва да се отбележи, като увеличим първоначално зададения с 1. Трябва да проверим, дали той не е станал по-голям от 12 и ако е така, да коригираме. Тъй като няма как да прескочим повече от един месец, когато увеличаваме с 5 дни, долната проверка е достатъчна.
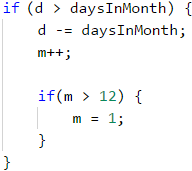
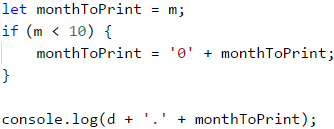
Остава само да принтираме резултата на конзолата. Важно е да форматираме изхода правилно, за да се появява водещата нула в първите 9 месеца. Това става, като създадем допълнителна променлива за месеца, към която да прибавим 0 при необходимост. Накрая принтираме деня и новата променлива за месеца.
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#4.
Задача: суми от 3 числа
Дадени са 3 цели числа. Да се напише програма, която проверява дали сумата на две от числата е равна на третото. Например, ако числата са 3, 5 и 2, сумата на две от числата е равна на третото: 2 + 3 = 5.
Входни данни
Като параметри на функцията подаваме три цели числа. Числата са в диапазона [1 … 1000].
Изходни данни
- Да се отпечата на конзолата един ред, съдържащ решението на задачата във формат "a + b = c", където a, b и c са измежду входните три числа и a ≤ b.
- Ако задачата няма решение, да се отпечата “No” на конзолата.
Примерен вход и изход
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 3 5 2 |
2 + 3 = 5 | 2 2 4 |
2 + 2 = 4 |
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 1 1 5 |
No | 2 6 3 |
No |
Насоки и подсказки
Приемаме си входа от конзолата.
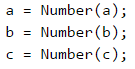
Трябва да проверим дали сумата на някоя двойка числа е равна на третото. Имаме три възможни случая:
- a + b = c
- a + c = b
- b + c = a
Ще си напишем рамка, която после ще допълним с нужния код. Ако никое от горните три условия не е изпълнено, ще зададем на програмата да принтира "No".

Сега остава да разберем реда, в който ще се изписват двете събираеми на изхода на програмата. За целта ще направим вложено условие, което проверява кое от двете числа е по-голямото. При първия случай, ще стане по този начин:
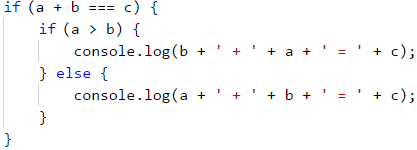
Аналогично, ще допълним и другите два случая. Пълният код на проверките и изходът на програмата ще изглеждат така:

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#5.
Задачи с единичен цикъл
Четвъртата задача на практическия изпит по “Основи на програмирането” включва единичен цикъл с проста логика в него. Ето няколко примера:
Задача: суми през 3
Дадени са n цели числа a1, a2, …, an. Да се пресметнат сумите:
- sum1 = a1 + a4 + a7 + … (сумират се числата, започвайки от първото със стъпка 3).
- sum2 = a2 + a5 + a8 + … (сумират се числата, започвайки от второто със стъпка 3).
- sum3 = a3 + a6 + a9 + … (сумират се числата, започвайки от третото със стъпка 3).
Входни данни
Като параметър на функцията подаваме масив с големина n+1 (0 ≤ n ≤ 1000). Масивът ще съдържа броя на числата n и n цели числа в интервала [-1000 … 1000]: a1, a2, …, an.
Изходни данни
На конзолата трябва да се отпечатат 3 реда, съдържащи търсените 3 суми, във формат като в примерите.
Примерен вход и изход
| Вход | Изход | Вход | Изход | Вход | Изход |
|---|---|---|---|---|---|
| 2 3 5 |
sum1 = 3 sum2 = 5 sum3 = 0 |
4 7 -2 6 12 |
sum1 = 19 sum2 = -2 sum3 = 6 |
5 3 5 2 7 8 |
sum1 = 10 sum2 = 13 sum3 = 2 |
Насоки и подсказки
Ще вземем броя на числата (големината на входния масив) и ще декларираме начални стойности на трите суми.

Тъй като не знаем предварително колко числа ще обработваме, ще си ги взимаме едно по едно в цикъл, който ще се повтори n на брой пъти и ще ги обработваме в тялото на цикъла.

За да разберем в коя от трите суми трябва да добавим числото, ще разделим поредния му номер на три и ще използваме остатъка. Ще използваме променливата i, която следи броя завъртания на цикъла, за да разберем на кое поред число сме. Когато остатъкът от i/3 е нула, това означава, че ще добавяме това число към първата сума, когато е 1 към втората и когато е 2 към третата.

Накрая, ще отпечатаме резултата на конзолата в изисквания формат.

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#6.
Задача: поредица от нарастващи елементи
Дадена е редица от n числа: a1, a2, …, an. Да се пресметне дължината на най-дългата нарастваща поредица от последователни елементи в редицата от числа.
Входни данни
Като параметър на функцията подаваме масив с големина n+1 (0 ≤ n ≤ 1000). Масивът ще съдържа броя на числата n и n цели числа в интервала [-1000 … 1000]: a1, a2, …, an.
Изходни данни
На конзолата трябва да се отпечата едно число – дължината на най-дългата нарастваща редица.
Примерен вход и изход
| Вход | Изход | Вход | Изход | Вход | Изход | Вход | Изход |
|---|---|---|---|---|---|---|---|
| 3 5 2 4 |
2 | 4 2 8 7 6 |
2 | 4 1 2 4 4 |
3 | 4 5 6 7 8 |
4 |
Насоки и подсказки
За решението на тази задача трябва да помислим малко по-алгоритмично. Дадена ни е редица от числа и трябва да проверяваме дали всяко следващо, ще бъде по-голямо от предното и ако е така да броим колко дълга е редицата, в която това условие е изпълнено. След това трябва да намерим коя редица от всички такива е най-дълга. За целта, нека да си направим няколко променливи, които ще ползваме през хода на задачата.
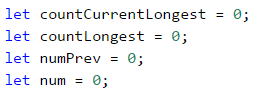
Променливата n е броя числа, които ще получим от конзолата. В countCurrentLongest ще запазваме броя на елементите в нарастващата редица, която броим в момента. Напр. при редицата: 5, 6, 1, 2, 3 countCurrentLongest ще бъде 2, когато сме стигнали втория елемент от броенето (5, 6, 1, 2, 3) и ще стане 3, когато стигнем последния елемент (5, 6, 1, 2, 3), понеже нарастващата редица 1, 2, 3 има 3 елемента. Ще използваме countLongest, за да запазим най-дългата нарастваща редица. Останалите променливи са num - числото, на което се намираме в момента, и numPrev - предишното число, което ще сравним с num, за да разберем дали редицата расте.
Започваме да въртим числата и проверяваме дали настоящото число а е по-голямо от предходното numPrev. Ако това е изпълнено, значи редицата е нарастваща и трябва да увеличим броя ѝ с 1. Това запазваме в променливата, която следи дължината на редицата, в която се намираме в момента, а именно - countCurrentLongest. Ако числото num не е по-голямо от предходното, това означава, че започва нова редица и трябва да стартираме броенето от 1. Накрая, след всички проверки, numPrev става числото, което използваме в момента, и започваме цикъла от начало със следващото въведено num.
Ето и примерна реализация на описания алгоритъм:
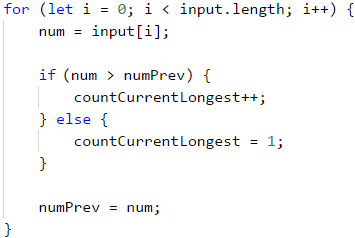
Остава да разберем коя от всички редици е най-дълга. Това ще направим с проверка в цикъла дали редицата, в която се намираме в момента, е станала по-дълга от дължината на най-дългата намерена до сега. Целият цикъл ще изглежда така:
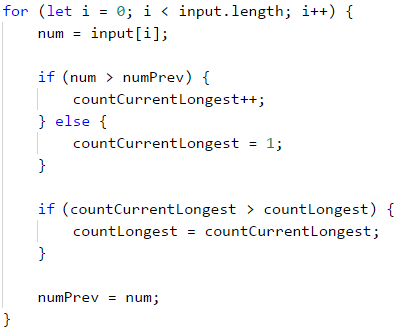
Накрая принтираме дължината на най-дългата намерена редица.
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#7.
Задачи за чертане на фигурки на конзолата
Петата задача на практическия изпит по “Основи на програмирането” изисква използване на един или няколко вложени цикъла за рисуване на някаква фигурка на конзолата. Може да се изискват логически размишления, извършване на прости пресмятания и проверки. Задачата проверява способността на студентите да мислят логически и да измислят прости алгоритми за решаване на задачи, т.е. да мислят алгоритмично. Ето няколко примера за изпитни задачи:
Задача: перфектен диамант
Да се напише функция, която приема като параметър цяло число n и чертае перфектен диамант с размер n като в примерите по-долу.
Входни данни
Параметър цяло число n в интервала [1 … 1000].
Изходни данни
На конзолата трябва да се отпечата диамантът като в примерите.
Примерен вход и изход
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 2 | * *-* * |
3 | * *-* *-*-* *-* * |
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 4 | * *-* *-*-* *-*-*-* *-*-* *-* * |
5 | * *-* *-*-* *-*-*-* *-*-*-*-* *-*-*-* *-*-* *-* * |
Насоки и подсказки
В задачите с чертане на фигурки най-важното, което трябва да преценим е последователността, в която ще рисуваме. Кои елементи се повтарят и с какви стъпки. Ясно може да забележим, че горната и долната част на диаманта са еднакви. Най-лесно ще решим задачата, като направим един цикъл, който чертае горната част, и след това още един, който чертае долната (обратно на горната).
Ще си прочетем числото n от параметрите на функцията.

Започваме да рисуваме горната половина на диаманта. Ясно виждаме, че всеки ред започва с няколко празни места и *. Ако се вгледаме по-внимателно, ще забележим, че празните места са винаги равни на n - индекса на реда - 1 (на първия ред са n-1, на втория - n-2 и т.н.) Ще започнем с това да нарисуваме броя празни места, както и първата звездичка. Забележете, че започваме да броим от 0, а не от 1. След това ще остане само да добавим няколко пъти -*, за да довършим реда.
Ето фрагмент от кода за начертаване на горната част на диаманта:
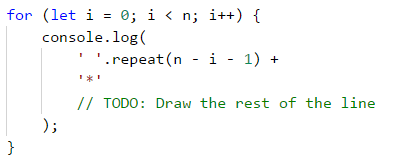
Остава да довършим всеки ред с нужния брой -* елементи. На всеки ред трябва да добавим i такива елемента (на първия -> 0, на втория -> 1 и т.н.)
Ето и пълния код за начертаване на горната част на диаманта:

За да изрисуваме долната част на диаманта, трябва да обърнем горната на обратно. Ще броим от n - 2, тъй като ако започнем от n - 1, ще изрисуваме средния ред два пъти. Не забравяйте да смените стъпката от ++ на --.
Ето го и кода за начертаване на долната част на диаманта:

Остава да си сглобим цялата програма като първо четем параметъра на функцията, печатаме горната част на диаманта и след него и долната част на диаманта.
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#8.
Задача: правоъгълник със звездички в центъра
Да се напише функция, която приема като параметър цяло число n и чертае правоъгълник с размер n с две звездички в центъра, като в примерите по-долу.
Входни данни
Параметърът е цяло число n в интервала [2 … 1000].
Изходни данни
На конзолата трябва да се отпечата правоъгълникът като в примерите.
Примерен вход и изход
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 2 | %%%%%**%%%%% |
3 | %%%%%%% %% ** %% %%%%%%% |
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 4 | %%%%%%%%% %% ** %% %%%%%%%%% |
5 | %%%%%%%%%%% %% %% ** %% %% %%%%%%%%%%% |
Насоки и подсказки
Прочитаме входния параметър на функцията.
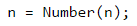
Първото нещо, което лесно забелязваме, е че първият и последният ред съдържат 2 * n символа %. Ще започнем с това и после ще нарисуваме средата на четириъгълника.

От дадените примери виждаме, че средата на фигурата винаги има нечетен брой редове. Забелязваме, че когато е зададено четно число, броят на редовете е равен на предишното нечетно (2 -> 1, 4 -> 3 и т.н.). Създаваме си променлива, която представлява броя редове, които ще има нашият правоъгълник, и я коригираме, ако числото n е четно. След това ще нарисуваме правоъгълника без звездичките. Всеки ред има за начало и край символа % и между тях 2 * n - 2 празни места (ширината е 2 * n и вадим 2 за двата процента в края). Не забравяйте да преместите кода за последния ред след цикъла.

Можем да стартираме и тестваме кода до тук. Всичко без двете звездички в средата трябва да работи коректно.
Сега остава в тялото на цикъла да добавим и звездичките. Ще направим проверка дали сме на средния ред. Ако сме на средния, ще рисуваме реда заедно със звездичките, ако не - ще рисуваме нормален ред. Редът със звездичките има n - 2 празни места (n е половината дължина и махаме звездичката и процента), две звезди и отново n - 2 празни места. Двата процента в началото и в края на реда си ги оставяме извън проверката.

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#9.
Задачи с вложени цикли с по-сложна логика
Последната (шеста) задача от практическия изпит по “Основи на програмирането” изисква използване на няколко вложени цикъла и по-сложна логика в тях. Задачата проверява способността на студентите да мислят алгоритмично и да решават нетривиални задачи, изискващи съставянето на цикли. Следват няколко примера за изпитни задачи.
Задача: четворки нарастващи числа
По дадена двойка числа a и b да се генерират всички четворки n1, n2, n3, n4, за които a ≤ n1 < n2 < n3 < n4 ≤ b.
Входни данни
Като параметри на функцията получаваме две цели числа a и b в интервала [0 … 1000].
Изходни данни
Изходът съдържа всички търсени четворки числа, в нарастващ ред, по една на ред.
Примерен вход и изход
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 3 7 |
3 4 5 6 3 4 5 7 3 4 6 7 3 5 6 7 4 5 6 7 |
15 20 |
15 16 17 18 15 16 17 19 15 16 17 20 15 16 18 19 15 16 18 20 15 16 19 20 15 17 18 19 15 17 18 20 15 17 19 20 15 18 19 20 16 17 18 19 16 17 18 20 16 17 19 20 16 18 19 20 17 18 19 20 |
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 5 7 |
No | 10 13 |
10 11 12 13 |
Насоки и подсказки
Прочитаме входните параметри на функцията. Създаваме и допълнителната променлива count, която ще следи дали има съществуваща редица числа.
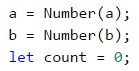
Най-лесно ще решим задачата, ако логически я разделим на части. Ако се изисква да изведем всички редици от едно число между a и b, ще го направим с един цикъл, който изкарва всички числа от а до b. Нека помислим как ще стане това с редици от две числа. Отговорът е лесен - ще ползваме вложени цикли.

Можем да тестваме недописаната програма, за да проверим дали е вярна до този момент. Тя трябва да отпечата всички двойки числа i, j, за които i ≤ j.
Тъй като всяко следващо число от редицата трябва да е по-голямо от предишното, вторият цикъл ще се върти от i + 1 (следващото по-голямо число). Съответно, ако не съществува редица от две нарастващи числа (a и b са равни), вторият цикъл няма да се изпълни и няма да се разпечата нищо на конзолата.
Аналогично, остава да реализираме по същия начин вложените цикли и за четири числа. Ще добавим и увеличаване на брояча, който инициализирахме в началото, за да знаем дали съществува такава редица.
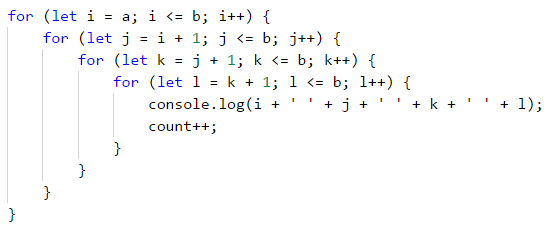
Накрая ще проверим дали броячът е равен на 0 и съответно ще принтираме “No” на конзолата, ако е така.
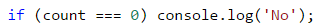
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#10.
Задача: генериране на правоъгълници
По дадено число n и минимална площ m да се генерират всички правоъгълници с цели координати в интервала [-n…n] с площ поне m. Генерираните правоъгълници да се отпечатат в следния формат:
(left, top) (right, bottom) -> area
Правоъгълниците се задават чрез горния си ляв и долния си десен ъгъл. В сила са следните неравенства:
- -n ≤ left < right ≤ n
- -n ≤ top < bottom ≤ n
Входни данни
Като параметри на функцията получаваме две числа:
- Цяло число n в интервала [1 … 100] – задава минималната и максималната координата на връх.
- Цяло число m в интервала [0 … 50 000] – задава минималната площ на генерираните правоъгълници.
Изходни данни
- На конзолата трябва да се отпечатат описаните правоъгълници във формат като в примерите по-долу.
- Ако за числата n и m няма нито един правоъгълник, да се изведе “No”.
- Редът на извеждане на правоъгълниците е без значение.
Примерен вход и изход
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 1 2 |
(-1, -1) (0, 1) -> 2 (-1, -1) (1, 0) -> 2 (-1, -1) (1, 1) -> 4 (-1, 0) (1, 1) -> 2 (0, -1) (1, 1) -> 2 |
2 17 |
No |
| Вход | Изход |
|---|---|
| 3 36 |
(-3, -3) (3, 3) -> 36 |
Насоки и подсказки
Прочитаме входните параметри на функцията. Ще създадем и един брояч, в който ще пазим броя на намерените правоъгълници.
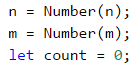
Изключително важно е да успеем да си представим задачата, преди да започнем да я решаваме. В нашия случай се изисква да търсим правоъгълници в координатна система. Нещото, което знаем е, че лявата точка винаги ще има координата х, по-малка от дясната. Съответно горната винаги ще има по-малка координата у от долната. За да намерим всички правоъгълници, ще трябва да направим цикъл, подобен на този от предходната задача, но този път не всеки следващ цикъл ще започва от следващото число, защото някои от координатите може да са равни (например left и top).

С променливите left и right ще следим координатите по хоризонталата, а с top и bottom - по вертикалата. Важното тук е да знаем кои координати кои са, за да можем да изчислим правилно страните на правоъгълника. Сега трябва да намерим лицето на правоъгълника и да направим проверка дали то е по-голямо или равно на m. Едната страна ще е разликата между left и right, а другата - между top и bottom. Тъй като координатите евентуално може да са разменени, ще ползваме абсолютни стойности. Отново добавяме и брояча в цикъла, като броим само четириъгълниците, които изписваме. Важно е да забележим, че поредността на изписване е left, top, right, bottom, тъй като така е зададено в условието.

Накрая принтираме “No”, ако не съществуват такива правоъгълници.

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/939#11.